Pravděpodobnost

Náhodné pokusy

Pravděpodobnost se zabývá matematickými zákonitostmi, které se projevují v náhodných pokusech. Tyto zákonitosti mají opodstatnění jen při dostatečně velkém počtu pokusů.

Náhodné pokusy jsou pokusy, které při dodržení předepsaných podmínek mohou vést k různým výsledkům. Tyto výsledky závisí nejen na předepsaných podmínkách, ale také na náhodě.

Množina možných výsledků pokusu a jevy

U každého náhodného pokusu jsme schopni předem vyjmenovat všechny možné výsledky, a to tak, že se navzájem vylučují a že jeden z nich nastane vždy. Tuto množinu možných výsledků označujeme  , její libovolný prvek .

Podmnožiny množiny možných výsledků nazýváme jevy.

Označujeme A, B, C, ....

Prázdná množina  se nazývá nemožný jev.

Množinu  nazýváme jistý jev.

O jevech platí vše co platí o množinách:

-         Je-li , říkáme, že výsledek  je příznivý jevu A

-         Je-li , říkáme, že jev A je podjevem jevu B

-         Jev  (sjednocení jevů A a B) nastává právě tehdy, nastane-li alespoň jeden z jevů A nebo B

-         Jev (průnik jevů A a B) nastává tehdy, nastanou-li oba jevy A i B

-         Je-li , říkáme, že se jevy A a B navzájem vylučují

-         Jev A´, který nastává právě tehdy, když jev A nenastává nazýváme jevem opačným k jevu A v množině  

Mějme nějaký pokus s množinou výsledků . Proveďme tento pokus celkem n-krát a pro každý možný výsledek  zaznamenejme, kolik pokusů skončilo právě tímto výsledkem. Toto číslo nazveme četnost výsledků . Podíl 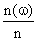 nazveme relativní četností výsledku . Pro toto číslo platí .

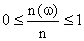Má-li náhodný pokus m různých výsledků a jsou-li tyto výsledky stejně možné (nebo stejně pravděpodobné), pak o každém z nich řekneme, že má pravděpodobnost .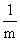

Mějme náhodný pokus a množinu možných výsledků . Pravděpodobnost  těchto výsledků jsou nezáporná čísla, jejichž součet je roven 1.

Pravděpodobnosti jevů

Pravděpodobnost jevu A označujeme P(A). Je definována jako součet pravděpodobností výsledků příznivých jevu A. Je tedy .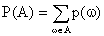

Má-li pokus m stejně pravděpodobných výsledků, je 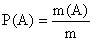, kde m(A) je počet výsledků příznivých jevu A.

Z této definice vyplývá, že:

·        pravděpodobnost nemožného jevu je rovna 0, tj.

·        pravděpodobnost jistého jevu je rovna 1, tj.

·        pro pravděpodobnost libovolného jevu A platí  

Sčítání pravděpodobností

Nechť jevy A a B se navzájem vylučují. Pravděpodobnost sjednocení dvou navzájem se vylučujících jevů je  

Jsou-li A₁, A₂, ......., A_r navzájem se vylučující jevy, tj. 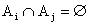 pro 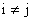, potom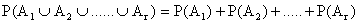

Jsou-li jevy A a B navzájem se nevylučující, tj. 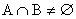, potom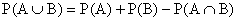

Jsou-li jevy A, B, C navzájem se nevylučující, potom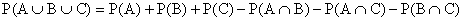

Nezávislé jevy

Nezávislostí dvou jevů rozumíme to, že uskutečnění jednoho nemá vliv na uskutečnění nebo neuskutečnění druhého jevu.

Řekneme, že jevy A a B jsou nezávislé, jestliže platí:

Bernoulliho schema

Mějme n nezávislých pokusů, z nichž každý skončí buď zdarem s pravděpodobností p nebo nezdarem s pravděpodobností q. Potom pravděpodobnost jevu A_k, že právě k pokusů bude zdařilých je: