Kuželosečky

Kružnice

Definice:

Kružnice je množina všech bodů v rovině, které mají od daného bodu roviny S [m, n] (středu kružnice) danou kladnou vzdálenost r (poloměr kružnice).


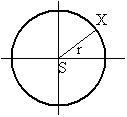
Bod X [x, y] je bodem kružnice k právě tehdy, když platí  


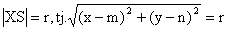
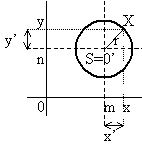
Kružnice se středem S [m, n] a s poloměrem r > 0 má rovnici

 
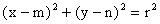
(středový tvar rovnice kružnice)

Tuto rovnici můžeme vyjádřit ve tvaru


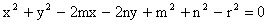
nebo-li

 
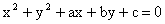
(obecný tvar rovnice kružnice),

kde a, b, c jsou reálná čísla.

Vnitřní a vnější body kružnice

Jestliže pro souřadnice bodu X [x, y] platí

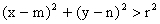, pak bod X leží vně kružnice (vnější bod kružnice)

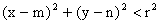, pak bod X leží uvnitř kružnice (vnitřní bod kružnice)

Kružnice a přímka:

Vzájemnou polohu řešíme jako  soustavu  dvou rovnic – lineární (přímka) a kvadratické (kružnice).

Přímka může být  tečnou (1 společný bod), sečnou (2 společné body) nebo může ležet mimo kružnici (0 společných bodů).

Rovnice tečny ke kružnici má tvar:


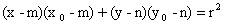 , kde  T [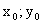] je bod dotyku.

Polára je  přímka daná rovnicí: 



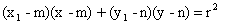
Leží na ní body dotyku tečen vedených bodem X [x1; y1] ke kružnici; nazýváme ji polára bodu

X vzhledem ke kružnici k.

Kulová plocha – sféra je množina všech bodů X [x; y; z] v prostoru, které mají od daného bodu S[m; n; p] (středu kulové

plochy ) vzdálenost r (poloměr kulové plochy). Její rovnice má tvar:

(x – m)2 + (y – n)2 – (z – p)2 = r2;   


Tečná rovina je rovina, která má s kulovou plochou 1 společný bod, bod dotyku T [x0; y0; z0]. Její rovnice má tvar:

(x – m)(x0 – m) + (y – n)(y0 – n) + (z0 – p)(z – p) =r2

Elipsa

Definice:

V rovině jsou dány body F1, F2 a je dáno číslo a tak, že 2a > .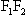

Elipsou rozumíme množinu všech bodů X uvažované roviny, pro které je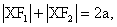


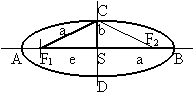
Body F1, F2 jsou tzv. ohniska elipsy, číslu a se říká hlavní poloosa elipsy.

F1, F2 .......................................ohniska elipsy

a...............................................hlavní poloosa

b...............................................vedlejší poloosa

e...............................................excentricita (výstřednost)  -   platí e2 = a2 - b2

S...............................................střed elipsy

A,B ..........................................hlavní vrcholy elipsy

C,D..........................................vedlejší vrcholy elipsy

Rovnice elipsy

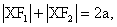  X [x, y]

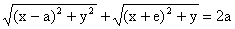
Po dosazení souřadnic ohnisek F1 [e, 0], F2 [- e, 0] dostáváme rovnost


                                                                                          
a po úpravách

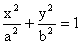                                 S [0, 0]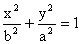                               

                                      hlavní osa totožná s x                                            hlavní osa totožná s y


Jestliže střed elipsy neleží v počátku - má souřadnice S [m, n], pak rovnice elipsy má tvar:

                                       

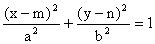
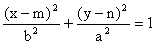
                                    hlavní osa rovnoběžná s x                                       hlavní osa rovnoběžná s y

(středová rovnice elipsy)

                              
Souřadnice ohnisek:

                                   F1 [m + e, n], F2 [m - e, n]                                     F1 [m, n + e], F2 [m, n - e]


Úpravou rovnic dostáváme:

 

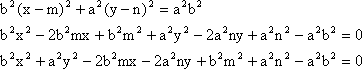
Po přeznačení získáme obecnou rovnici elipsy ve tvaru:

px2 + qy2 + 2rx + 2sy + t = 0, kde pq>0

Elipsa a přímka:

Vzájemnou polohu řešíme jako  soustavu  dvou rovnic – lineární (přímka) a kvadratické (kružnice).

Přímka může být  tečnou (1 společný bod), sečnou (2 společné body) nebo může ležet mimo elipsu (0 společných bodů).

Rovnice tečny k elipse má tvar:


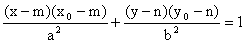     (hlavní osa rovnoběžná s osou x)
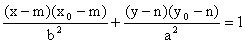                            popř.     (hlavní osa rovnoběžná s osou y),


 kde  T [x0; y0] je bod dotyku.

Hyperbola

Definice:

Hyperbola je množina všech bodů v rovině, které mají tu vlastnost, že absolutní hodnota rozdílu jejich vzdáleností od dvou daných různých bodů je rovna kladné konstantě.

Tyto body označujeme F1, F2 a nazýváme ohniska hyperboly, přímka F1F2 se nazývá hlavní osa hyperboly, střed S [m; n] úsečky F1F2 nazýváme  střed hyperboly.  Vzdálenost bodů F1, F2 se označuje zpravidla 2e, číslo 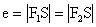se nazývá výstřednost hyperboly. Kolmice k hlavní ose vedená středem S hyperboly se nazývá vedlejší osa hyperboly        

Průsečíky A, B hyperboly s její hlavní osou se nazývají vrcholy hyperboly.

   Absolutní hodnota rozdílu vzdáleností bodů X [x; y] hyperboly od jejích ohnisek se zpravidla označuje 2a (a>0), a je velikost hlavní poloosy hyperboly. Číslo 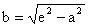 se nazývá velikost vedlejší poloosy. Pro libovolný bod  X [x; y] hyperboly platí podle definice

.
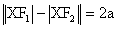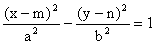S využitím vztahu pro výpočet vzdálenosti dvou bodů můžeme tento vztah (po rozepsání do souřadnic) upravit na středový tvar rovnice hyperboly

    (střed S [m; n], hlavní osa rovnoběžná s osou x)

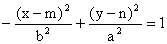  (střed S [m; n], hlavní osa rovnoběžná s osou y)

Obecnou rovnici hyperboly získáme úpravou předchozích rovnic a přeznačením ve tvaru:
px2 + qx2 + 2rx + 2sy + t = 0, kde pq< 0
Hyperbola a přímka

Vzájemnou polohu přímky a hyperboly zjišťujeme řešením soustavy jejich rovnic.

Rovnice tečny v bodě T [x0; y0] má tvar:

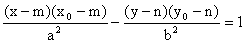      (osa hyperboly rovnoběžná s osou x)

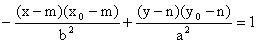   (osa hyperboly rovnoběžná s osou y)

Rovnice asymptoty hyperboly má tvar:

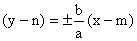  (osa hyperboly rovnoběžná s osou x)

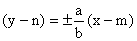  (osa hyperboly rovnoběžná s osou y)

Asymptoty jsou přímky, které  procházejí středem hyperboly a nemají s ní žádný společný bod.


Parabola

Definice:

Parabola je množina všech bodů X roviny, které mají stejnou vzdálenost od daného bodu F a od dané přímky d, F 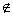d.
Bod F se nazývá ohnisko paraboly, přímka d řídící přímka paraboly. Přímka o vedená ohniskem F kolmo k řídící přímce d se nazývá osa paraboly. Vzdálenost p ohniska F od řídící přímky d se nazývá parametr paraboly, p = 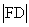. Vrchol paraboly je střed úsečky FD.

Je-li V [m; n],  je vrcholová rovnice paraboly

(y - n)2 = 2p(x - m)           (osa o rovnoběžná s kladným směrem osy x)
       
(y - n)2 = - 2p(x - m)        (osa o rovnoběžná se záporným směrem osy x)

(x - m)2 = 2p(y - n)           (osa o rovnoběžná s kladným směrem osy y)

(x - m)2 = - 2p(y - n)         (osa o rovnoběžná se záporným směrem osy y)

a obecná rovnice paraboly

y2 + 2rx + 2sy + t = 0,  r0      (osa o rovnoběžná s osou x)

x2 + 2rx + 2sy + t = 0 , s0      (osa o rovnoběžná s osou y)


Parabola a přímka

Rovnice tečny paraboly v bodě T [x0; y0] má tvar

(y - n)(y0 - n) = p(x + x0 - 2m)        (osa o rovnoběžná s kladným směrem osy  x)

(y - n)(y0 - n) = - p(x + x0 - 2m)      (osa o rovnoběžná se záporným směrem osy x)

(x - m)(x0 - m) = p(y + y0 - 2n)       (osa o rovnoběžná s kladným směrem osy y)

(x - m)(x0 - m) = - p(y + y0 - 2n)     (osa o rovnoběžná se záporným směrem osy y)