Přímka a rovina

Parametrická rovnice přímky, polopřímky a úsečky v rovině

• Uvažujme případ, kdy přímka p je určena jedním bodem A [x_A, y_A] a směrovým vektorem u = (u₁, u₂).

Rovnici p: X = A + tu, kde tR, nazýváme parametrické (vektorové) vyjádření přímky p.

Bod X je každý bod přímky p, bod A je určující bod přímky p, u je směrový vektor přímky p, t je parametr, který necháme proběhnout celou množinou R.

Symbolickou rovnici přímky můžeme rozepsat pomocí souřadnic

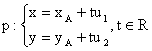
• Uvažujme případ, kdy přímka je určena dvěma různými body A [x_A, y_A] a

B [x_B, y_B]. Určíme směrový vektor u = B – A a můžeme symbolickou rovnici přímky p psát ve tvaru X = A + t.(B – A), tR.

Rozepíšeme ji pomocí souřadnic a dostaneme

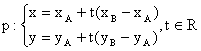
Stejnými rovnicemi můžeme popsat polopřímku AB a úsečku AB.

Rovnici X = A + t(B – A), kde , nazýváme parametrické (vektorové) vyjádření polopřímky AB.

Rovnici X = A + t(B – A), kde , nazýváme parametrické (vektorové) vyjádření úsečky AB.

Velikost úsečky AB určíme stejně jako velikost vektoru AB:

Střed úsečky AB lze určit tímto způsobem:

Obecná rovnice přímky v rovině

Obecnou rovnici přímky p v rovině dostaneme z jejich parametrických rovnic tak, že vyloučíme parametr t.

Obecná rovnice přímky p je pak p: ax + by + c = 0, kde x, y jsou souřadnice libovolného bodu přímky p, čísla a, b, c jsou reálná čísla, pro něž musí platit

[a, b] [0, 0].

V obecné rovnici přímky jsou čísla a, b souřadnicemi tzv. normálového vektoru n přímky p.

Normálový vektor n = (a, b) je vektor kolmý ke směrovému vektoru u přímky p.

Vztah mezi normálovým vektorem n a směrovým vektorem u přímky:

Je-li n = (a, b), pak je u = (- b, a) nebo u = (b, - a).

Všechny možnosti, které mohou nastat v obecné rovnici přímky

p: ax + by + c = 0 pro proměnné hodnoty a, b, c:

p: by = 0 resp. y = 0 Rovnice popisuje osu x.	p: by + c = 0 resp. y = q Rovnice popisuje přímku p||x	p: ax = 0 resp. x = 0 Rovnice popisuje osu y.
p: ax + c = 0 resp. x = r Rovnice popisuje přímku p||y	p: ax + by = 0 resp. y = kx Rovnice popisuje přímku p, která prochází počátkem systému souřadnic.	p: ax + by + c = 0 resp.y = kx +  q Rovnice popisuje přímku zcela obecně položenou v systému souřadnic.

Směrnicový tvar rovnice přímky v rovině

Směrnicový tvar rovnice přímky p je p: y = kx + q, kde k, q R.

Číslo k se nazývá směrnice přímky. Směrnicový tvar dostaneme z obecné rovnice přímky

p: ax + by + c = 0.

Je-li b0, můžeme celou rovnici dělit b a po úpravě dostaneme

Přímku nemůžeme popsat směrnicový tvarem, pokud je rovnoběžná s osou y (hodnota b = 0).

Tento směrnicový tvar rovnice přímky souvisí s pojmem směrový úhel , protože směrnice k je definována také jako .

Úhel .

Směrový úhel  je definován jako kladný orientovaný úhel, jehož počátečním ramenem je kladný směr osy x a koncovým ramenem je část přímky p.

Je-li přímka p určena body A [x_A, y_A], B [x_B, y_B], lze směrnicový tvar přímky p vyjádřit ve tvaru