Množiny bodů dané
vlastnosti
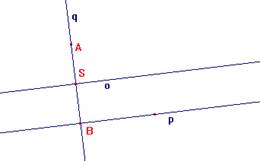
5.6. Je dána přímka p a bod A, který na ní neleží. Určete množinu středů všech úseček AX, kde X je libovolný bod přímky p.
Řešení:
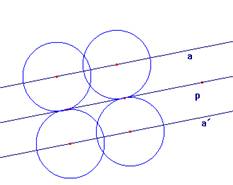
5.7. Určete množinu středů všech kružnic, které mají poloměr r a dotýkají se dané přímky p.
Řešení:
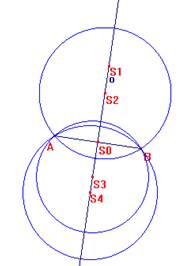
5.8. V rovině jsou dány dva různé body A, B. Určete množinu středů všech kružnic, které procházejí danými body A, B.
Řešení:
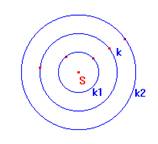
5.9. V rovině je dána kružnice k(S, R). Určete množinu středů všech kružnic, které se dotýkají kružnice k a mají poloměr r < R.
Řešení:
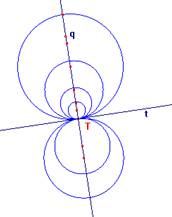
5.10. V rovině je dána přímka t a bod T
t. Určete množinu středů všech
kružnic, které se dotýkají přímky t v bodě T.
Řešení:
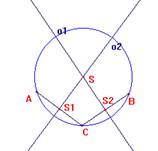
6.2. Sestrojte kružnici k(S, r), jsou-li dány její tři různé body A, B, C.
Řešení:
6.4. Jsou dány různoběžky a, b a body A a, B
a.
a) Sestrojte všechny kružnice, které se dotýkají přímek a, b a které procházejí bodem A.
b) Sestrojte všechny kružnice, které se dotýkají přímky a a procházejí body A, B.
Řešení:
a)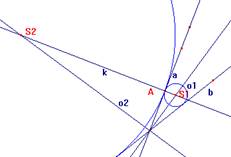 
b)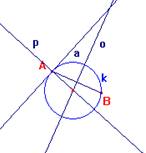 
G2.6. Najděte množinu všech bodů, ze kterých vidíme danou úsečku AB pod úhlem větším než 45° a menším než 60°.
G2.8. Jsou dány dva různé body A, B. Určete množinu vrcholů X všech tupých úhlů AXB.
G2.9. Jsou dány dvě rovnoběžky a, b. Najděte množinu všech bodů X, které mají od přímky a dvojnásobnou vzdálenost než od přímky b.
G2.10. Jsou dány dvě rovnoběžky a, b ve vzdálenosti