Limita posloupnosti a nekonečné řady

Pojem limita posloupnosti

Příklad:

Vypište prvních šest členů posloupnosti 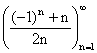a vyznačte jejich obrazy v soustavě souřadnic.

Řešení:

Na obrázku vidíme, že prvních šest členů posloupnosti se stále více přibližuje k číslu .

Jinak řečeno, zmenšuje se postupně absolutní hodnota rozdílu členu posloupnosti a čísla .

Vypočítáme si pro prvních šest členů posloupnosti:

	a tedy

Z výpočtů, které jsme provedli, bychom mohli usoudit, že např. pro všechna přirozená čísla

n 7 platí .

Obecně bychom to mohli dokázat následujícím způsobem:

Pro n-tý člen studované posloupnosti platí:

,

a tedy

.

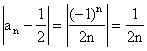Určíme nyní všechna nN, pro která platí:

,

čili

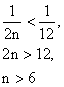
nebo-li

Pro všechna přirozená čísla 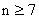je tedy skutečně .

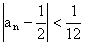· Říkáme, že posloupnost je konvergentní, právě když existuje číslo aR takové, že platí:

Ke každému > 0 existuje n₀N tak, že pro všechna přirozená čísla nn₀ je .

Číslo a se nazývá limita posloupnosti

Skutečnost, že posloupnost má limitu rovnou číslu a, zapisujeme

a čteme “limita a_n pro n jdoucí k nekonečnu je rovna a” nebo stručněji “limita a_n je a”.

Posloupnosti, které nejsou konvergentní, jsou divergentní.

Definici limity posloupnosti můžeme vyslovit také takto:

· Číslo a se nazývá limita posloupnosti , právě když ke každému číslu existuje n₀N tak, že pro všechna přirozená čísla nn₀ je .

Definici konvergentní posloupnosti můžeme uvést také takto:

· Říkáme, že posloupnost je konvergentní, právě když existuje číslo aR takové, že platí:

Ke každému > 0 existuje n₀N tak, že pro všechna přirozená čísla nn₀

je .

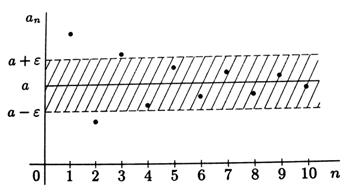
Ať zvolíme jakékoliv malé>0, vždy existuje n₀N, že pro všechna nn₀ patří obrazy členů posloupnosti v soustavě souřadnic do vnitřku pásu s “hranicemi” .

Platí následující věty:

· Každá posloupnost má nejvýše jednu limitu.

· Každá konvergentní posloupnost je omezená.

Věty o limitách posloupností

Jestliže posloupnosti , jsou konvergentní a přitom , pak je konvergentní i posloupnost

· a platí

· a platí

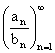· a platí

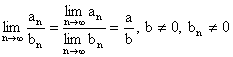
· a platí

· a platí

Geometrická posloupnost , pro kterou je , je konvergentní a její limita je rovna 0.