Definice posloupnosti

Posloupnost je funkce, jejímž definičním oborem je množina přirozených čísel N.

Posloupnost se nazývá nekonečná, pokud je definičním oborem celá množina N. Posloupnost se nazývá konečná, pokud je jejím definičním oborem množina prvních n přirozených čísel {1; 2; 3; ...; n}.

Funkční hodnoty posloupnosti se nazývají členy posloupnosti; funkční hodnota posloupnosti v bodě n 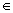N se nazývá n-tý člen posloupnosti a značí se  a_n.

Posloupnost (nekonečnou) zapisujeme 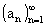nebo (a₁, a₂, a₃, ... a_n...). Konečnou posloupnost zapisujeme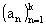
nebo (a₁, a₂, a₃, ..., a_k).

Vlastnosti posloupností

Posloupnost 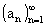se nazývá rostoucí, je-li a_n+1 > a_n, pro každé n 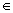N.
Posloupnost 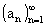se nazývá klesající, je-li a_n+1 < a_n, pro každé 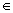n N.
Posloupnost 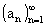se nazývá neklesající, je-li a_n+1  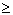a_n, pro každé 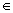n N.
Posloupnost 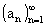se nazývá nerostoucí, je-li a_n+1  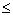a_n, pro každé 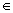n N.
Posloupnost 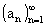se nazývá shora omezená, jestliže existuje takové reálné číslo h, že a_n 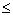h pro každé  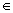n N.
Posloupnost 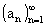se nazývá zdola omezená, jestliže existuje takové reálné číslo d, že a_n 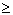d pro každé  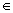n N.
Posloupnost 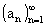se nazývá omezená, pokud je omezená shora i zdola.

Pozn.:
 Pod pojmem posloupnost rozumíme vždy posloupnost nekonečnou, pokud není uvedeno jinak.
Rostoucí, klesající, nerostoucí nebo neklesající posloupnost nazýváme souhrnně monotónní posloupnosti.
Posloupnosti rostoucí a klesající nazýváme souhrnně ryze monotónní posloupnosti.

Vyjádření posloupnosti

Posloupnost 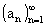můžeme zadat několika způsoby:
- Pokud je posloupnost zadána obecným vzorcem, který číslu n přiřadí číslo a_n, tedy číslu 1 přiřadí číslo a₁, číslu 2 člen a₂,  číslu 3 člen a₃ ..., říkáme, že posloupnost   je zadána vzorcem pro n-tý člen.
- Pokud je posloupnost zadána pomocí prvního členu (nebo několika prvních členů) posloupnosti a vzorcem, podle něhož lze určit další členy, říkáme, že posloupnost je zadána rekurentně.
- Pokud je posloupnost zadána pomocí několika prvních členů, říkáme, že je zadána výčtem prvků. Z naznačení prvních členů vyplývá, jak budou vypadat členy následující.
- Posloupnost je zadána graficky, pokud je dán její graf. Grafem posloupnosti je vždy množina izolovaných bodů. Posloupnost můžeme znazornit graficky buď v soustavě souřanic nebo na přímce.

Příklady:
Příklad posloupnosti zadané vzorcem pro n-tý člen je: .

Příklad posloupnosti zadané rekurentně je: a₁ = 6, a_n+1 = a_n - 3.

Příklad posloupnosti zadané výčtem prvků je: 1, 4, 7, 10, 13, 16, ...