Nekonečná geometrická řada.
Definice aritmetické posloupnosti
Aritmetická posloupnost je taková posloupnost, v níž je rozdíl následujícího členu a předchozího členu stálý. Tento rozdíl se nazývá diference a označuje se d
(d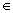 R).
R).
Rekurentní vzorec aritmetické posloupnosti je an+1 = an + d, kde n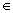 N.
N.
Obecný vzorec aritmetické posloupnosti je an = a1 + (n - 1)d.
Vzorec pro výpočet součtu prvních n členů
Pro každé dva členy ar, as aritmetické posloupnosti platí:
ar - as = (r - s)d
Pro součet prvních n členů aritmetické posloupnosti platí:

Definice geometrické posloupnosti
Geometrická posloupnost je taková posloupnost, v níž podíl následujícího a předchozího členu je konstantní.
Tento podíl se označuje q a nazývá se kvocient (q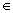 R).
R).
Rekurentní vorec geometrické posloupnosti je an+1 = an.q nebo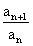 = q, kde n
= q, kde n 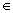 N.
N.
Obecný vzorec geometrické posloupnosti je an = a1.qn - 1.
Vzorec pro výpočet součtu prvních n členů
Pro každé dva členy geometrické posloupnosti ar, as platí:
ar = as.qr - s
Pro součet prvních n členů geometrické posloupnosti platí:
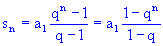 pro q
pro q 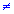 1 sn = n.a1 pro q = 1
1 sn = n.a1 pro q = 1
Definice nekonečné geometrické řady
Nekonečná geometrická řada je výraz a1 + a2 + a3 + ...... + an + ............,
jehož členy tvoří geometrickou posloupnost.
Nekonečnou geometrickou řadu lze také stručně zapsat výrazem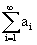 (čteme "suma všech ai pro i = 1 až nekonečno").
(čteme "suma všech ai pro i = 1 až nekonečno").
Vzorec pro součet nekonečné geometrické řady
Nekonečná geometrická řada a1 + a1q + a1q2 + a1q3 + ..... + a1qn + ...
- je konvergentní právě tehdy, je-li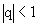 a pro její součet tedy platí:
a pro její součet tedy platí: 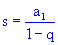
- je divergentní právě tehdy, je-li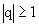
Aritmetická posloupnost je taková posloupnost, v níž je rozdíl následujícího členu a předchozího členu stálý. Tento rozdíl se nazývá diference a označuje se d
(d
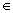 R).
R).Rekurentní vzorec aritmetické posloupnosti je an+1 = an + d, kde n
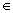 N.
N.Obecný vzorec aritmetické posloupnosti je an = a1 + (n - 1)d.
Vzorec pro výpočet součtu prvních n členů
Pro každé dva členy ar, as aritmetické posloupnosti platí:
ar - as = (r - s)d
Pro součet prvních n členů aritmetické posloupnosti platí:

Definice geometrické posloupnosti
Geometrická posloupnost je taková posloupnost, v níž podíl následujícího a předchozího členu je konstantní.
Tento podíl se označuje q a nazývá se kvocient (q
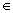 R).
R).Rekurentní vorec geometrické posloupnosti je an+1 = an.q nebo
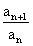 = q, kde n
= q, kde n 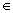 N.
N.Obecný vzorec geometrické posloupnosti je an = a1.qn - 1.
Vzorec pro výpočet součtu prvních n členů
Pro každé dva členy geometrické posloupnosti ar, as platí:
ar = as.qr - s
Pro součet prvních n členů geometrické posloupnosti platí:
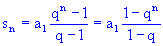 pro q
pro q  1 sn = n.a1 pro q = 1
1 sn = n.a1 pro q = 1Definice nekonečné geometrické řady
Nekonečná geometrická řada je výraz a1 + a2 + a3 + ...... + an + ............,
jehož členy tvoří geometrickou posloupnost.
Nekonečnou geometrickou řadu lze také stručně zapsat výrazem
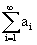 (čteme "suma všech ai pro i = 1 až nekonečno").
(čteme "suma všech ai pro i = 1 až nekonečno").Vzorec pro součet nekonečné geometrické řady
Nekonečná geometrická řada a1 + a1q + a1q2 + a1q3 + ..... + a1qn + ...
- je konvergentní právě tehdy, je-li
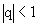 a pro její součet tedy platí:
a pro její součet tedy platí: 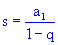
- je divergentní právě tehdy, je-li