Exponenciální
a logaritmické funkce, rovnice a nerovnice
Pojem
exponenciální funkce a její graf Exponenciální funkce o základu a je dána předpisem f: y = ax , kde a
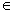 (0,1)
(0,1)  (1,
(1,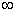 ).Grafem
exponenciální funkce je exponenciála.
).Grafem
exponenciální funkce je exponenciála.Druhy exponenciálních funkcí
Exponenciální funkce f: y = 10x se nazývá dekadická exponenciální funkce. Exponenciální funkce f: y = ex, kde základ je roven e (tzv. Eulerovo číslo, e = 2,718281…), se nazývá přirozená exponenciální funkce.
Vlastnosti exponenciální funkce f: y = ax v závislosti na jejím základu a:
a 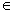 (1, (1,
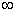 ) ) |
a 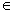 (0,1) (0,1) |
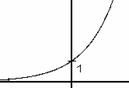 Df = R, Hf = (0, Funkce není sudá ani lichá. Funkce je zdola omezená. Je rostoucí, tedy prostá. Nemá maximum ani minimum. Graf prochází bodem [0, 1]. Osa
x je asymptotou
grafu
|
 Df = R, Hf = (0, Funkce není sudá ani lichá. Funkce je zdola omezená. Je klesající, tedy prostá. Nemá maximum ani minimum. Graf prochází bodem [0, 1]. Osa x je asymptotou grafu. |
Pojem logaritmická funkce a její graf
Logaritmická funkce o základu a , kde a
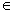 (0,1)
(0,1)  (1,
(1,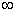 ), je inverzní
k exponenciální
funkci o témže základu a má předpis
), je inverzní
k exponenciální
funkci o témže základu a má předpisf: y = loga x. Grafem logaritmické funkce je logaritmická křivka.
Druhy logaritmických funkcí
Nejčastěji se vyskytují logaritmy se základem 10 a se základem e. Jedná se o tzv. dekadické logaritmy f: y = log10 x, píšeme log10 x = log x, a o tzv. přirozené logaritmy f: y = ln x, píšeme loge x = ln x.
Vlastnosti logaritmické funkce f: y = loga x v závislosti na jejím základu:
a 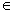 (1, (1,
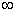 ) ) |
a 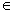 (0,1) (0,1) |
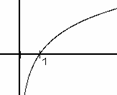 Hf = R, Df = (0, Funkce není sudá ani lichá. Funkce není zdola ani shora omezená. Je rostoucí, tedy prostá. Nemá maximum ani minimum. Graf prochází bodem [1, 0]. Osa
y je asymptotou
grafu.
|
 Hf = R, Df = (0, Funkce není sudá ani lichá. Funkce není zdola ani shora omezená. Je klesající, tedy prostá. Nemá maximum ani minimum. Graf prochází bodem [1, 0]. Osa
y je asymptotou
grafu.
|
Logaritmus čísla
Funkční hodnoty logaritmické funkce se nazývají logaritmy.
Logaritmus čísla b při základu a je číslo exponent x, na který musíme umocnit základ a, abychom dostali logaritmované číslo b.
Pro počítání s logaritmy používáme tyto vztahy:
Exponenciální rovnice a nerovnice
Exponenciální rovnice a nerovnice jsou rovnice a nerovnice, ve kterých se neznámá vyskytuje v exponentu.
Rovnice typu af(x) = ag(x) se řeší porovnáním exponentů.
Rovnice typu af(x) = bg(x) se řeší logaritmováním na tvar f(x) . log a = g(x) – log b
Příklady:


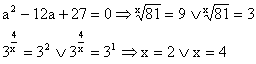
Logaritmické rovnice a nerovnice
Logaritmické rovnice a nerovnice jsou rovnice a nerovnice, které mají neznámou buď jako logaritmovaný výraz nebo se neznámá vyskytuje jako základ logaritmu.
Příklady:
rovnice:

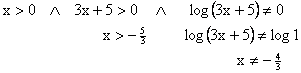
nerovnice: