 N.
N.Pojem mocninné funkce s přirozeným mocnitelem
Mocninná funkce s přirozeným mocnitelem je funkce určená předpisem f: y = xn , kde n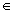 N.
N.
Druhy mocninných funkcí s přirozeným mocnitelem
Vlastnosti mocninných funkcí v závislosti na mocniteli n:
| n sudé | n liché |
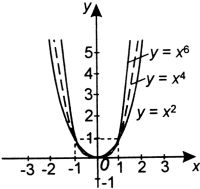 | 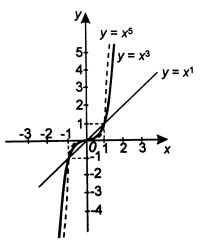 |
| Df = R Hf =  Je to funkce sudá. Je omezená zdola, shora omezená není. Pro x 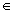 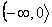 je klesající, je klesající,pro x 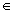  je rostoucí. je rostoucí.Má minimum v bodě [0; 0], maximum nemá. Není prostá. | Df = R Hf = R Je to funkce lichá. Není omezená shora ani zdola. Je rostoucí v celém Df, a tedy prostá. Nemá maximum ani minimum. |
Pojem mocninné funkce se záporným celočíselným mocnitelem
Mocninná funkce se záporným celočíselným mocnitelem je funkce určená předpisem f: y = x-n, kde n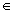 N.
N.| n sudé | n liché |
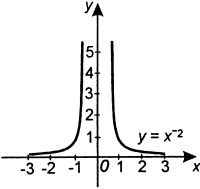 | 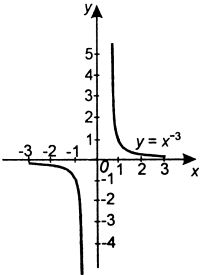 |
Df = 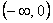  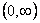 Hf = 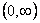 Je to funkce sudá. Je omezená zdola, shora omezená není. Pro x 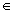 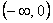 je rostoucí, je rostoucí,pro x 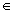 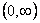 je klesající. je klesající.Nemá maximum ani minimum. Není prostá. | Df = 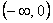  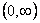 Hf = 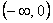  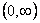 Je to funkce lichá. Není shora ani zdola omezená. Je klesající na celém Df. Nemá maximum ani minimum. Je prostá. |