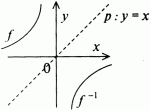Základní poznatky o funkcích

Pojem funkce reálné proměnné

Nechť jsou dány dvě neprázdné množiny reálných čísel A a B. Přiřadíme-li každému číslu podle nějakého předpisu právě jedno číslo (které označíme y = f(x) a nazveme funkční hodnota), pak množina f všech uspořádaných dvojic [x; f(x)] se nazývá reálná funkce reálné proměnné.

Zapisujeme f: y = f(x).

Množinu A označujeme D(f) a nazýváme ji definičním oborem funkce f. Přitom proměnnou  nazýváme nezávisle proměnná.

Množinu prvků , z nichž ke každému existuje alespoň jeden takový prvek , že [x ; y] f , nazýváme oborem hodnot funkce f a označujeme ji H(f).

Grafem funkce f v kartézské soustavě souřadnic je množina všech bodů roviny, které mají souřadnice [x; f(x)].

Funkce je jednoznačně určena, je-li určen její definiční obor a funkční předpis y = f(x). Tento předpis může být zadán:

- rovnicí

- grafem

- tabulkou

- slovním předpisem

Rovnost funkcí, operace s funkcemi

Jsou dány dvě funkce f a g s definičními obory D(f) a D(g) a platí

. Pak zavedeme na množině A:

rovnost funkcí f, g tak, že 

součet funkcí f, g tak, že 

rozdíl funkcí f, g tak, že

součin funkcí f, g tak, že 

podíl funkcí f, g tak, že

Složená funkce

Funkce F je složená, pokud ji můžeme zapsat ve tvaru F(x) = f(g(x)) pro všechna x . Funkci g(x) = u se říká vnitřní složka, funkci f(u) vnější složka složené funkce F.

Monotónnost funkce, prostá funkce

Je dána funkce f definovaná na množině . Jestliže pro všechna x, kde x₁ < x₂, platí:

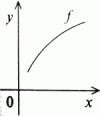
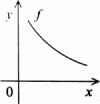
f(x₁) < f(x₂), pak se f nazývá funkce na A rostoucí                 f(x₁) > f(x₂), pak se f nazývá funkce na A klesající

pak se f nazývá funkce na A neklesající            pak se f nazývá funkce na A nerostoucí

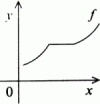
Funkce rostoucí a klesající se nazývají ryze monotónní.

Funkce neklesající a nerostoucí se nazývají monotónní.

Nechť je dána funkce f na množině . Pak f se nazývá na množině A prostá právě tehdy, když pro , kde , je .

Omezenost funkce, sudá a lichá funkce

Je-li f definovaná v množině , pak se nazývá:

funkce na A zdola omezená právě tehdy, když existuje takové číslo , že pro je

funkce na A shora omezená právě tehdy, když existuje takové číslo , že pro je

funkce na A omezená právě tehdy, když je omezená shora i zdola

Říkáme, že funkce f je sudá právě tehdy, když ke každému existuje a pro každé x a –x platí f(x) = f(-x).

Říkáme, že funkce f je lichá právě tehdy, když ke každému  existuje a pro každé x a –x platí
 - f(x) = f(-x).

Maxima a minima funkce

Je-li f funkce, , , pak má funkce f na A:

v bodě a minimum právě tehdy, když  je ,

v bodě b maximum právě tehdy, když   je .

Periodická funkce, inverzní funkce

Funkce f se nazývá periodická funkce, existuje-li takové , že pro platí:

1. je-li funkce definována v čísle x, pak je definována také v číslech x + kp

2. pro platí f(x) = f(x + kp).

Jestliže je funkce prostá v celém D(f) a má obor H(f), pak lze na H(f) definovat funkci, která každému  přiřazuje právě to číslo , pro které je f(x) = y.

Tato funkce se nazývá inverzní funkce k funkci f a značíme ji . Pro tyto funkce platí  a . Grafy těchto funkcí jsou osově souměrné podle přímky p: y = x.