Kvadratická funkce

Pojem kvadratická funkce a její graf

Kvadratickou funkcí nazýváme každou funkci danou předpisem f: y = ax² + bx + c,

kde a, b, c R a a 0. Grafem kvadratické funkce je parabola. Osa paraboly je rovnoběžná s osou y. Průsečík paraboly a osy paraboly nazýváme vrchol V paraboly.

 Druhy kvadratických funkcí

 Rozdělení kvadratických funkcí podle hodnoty koeficientu a:

a > 0	a < 0
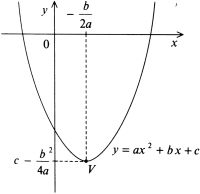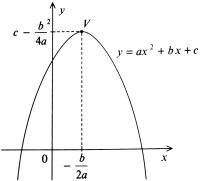Df = R, Hf = Funkce je zdola omezená, není shora omezená. Je rostoucí v , klesající v . V bodě x = má funkce minimum, maximum funkce nemá.	Df = R, Hf = Funkce je shora omezená, není zdola omezená. Je rostoucí v , klesající v . V bodě x = má funkce maximum, minimum nemá.

Je-li b = 0, má funkce tvar f: y = ax² + c a je sudá, tj. souměrná podle osy y.

Kvadratická funkce s absolutní hodnotou

Kvadratickou funkci s absolutní hodnotou řešíme podobně jako lineární funkce s absolutní hodnotou, tj. pomocí metody intervalů a nulových bodů.