Mnohočleny

Mnohočlenem o jedné proměnné xR nazýváme výraz

M(x) = anxn + an-1xn-1 + … + a1x + a0.

Čísla an, an-1, … , a1, a0 jsou reálná čísla a nazývají se koeficienty mnohočlenu.

Je-li an 0, pak číslo nN0, se nazývá stupeň mnohočlenu.

Mnohočlen M(x) o jedné proměnné x je součet jednotlivých členů mnohočlenu

anxn, an-1xn-1,  … ,a1x, a0.

Mnohočleny můžeme uspořádat vzestupně, tj. od nejvyšší mocniny k nejnižší, nebo sestupně, tj. naopak.

Mnohočlenem (polynomem) o m proměnných nazýváme součet konečného počtu členů tvaru

. Stupeň polynomu o více proměnných je nejvyšší součet mocnitelů proměnných v jednotlivých členech.

Rovnost mnohočlenů

Dva mnohočleny o jedné proměnné jsou si rovny, tj. M(x) = N(x), právě tehdy, jsou-li si rovny koeficienty členů, které mají stejný stupeň.

Operace s mnohočleny

Sčítání mnohočlenů provádíme tak, že sčítáme jednotlivé členy, které mají proměnné se stejným exponentem.

Odčítání mnohočlenů provádíme tak, že přičítáme mnohočlen opačný, tj. mnohočlen, který vznikne z daného mnohočlenu změnou znaménka v opačné u všech koeficientů.

Násobení mnohočlenu jednočlenem provádíme tak, že tímto jednočlenem násobíme každý člen mnohočlenu, a je-li to možné, vzniklé součiny sečteme.

Násobení mnohočlenu mnohočlenem provádíme tak, že každý člen jednoho mnohočlenu vynásobíme každým členem druhého a vzniklé součiny sečteme.

Při počítání s mnohočleny je výhodné užívat vztahy:

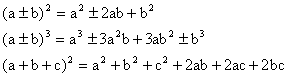
Dělení mnohočlenu jednočlenem provádíme tak, že každý člen mnohočlenu dělíme jednočlenem.

Dělení mnohočlenu mnohočlenem – viz. příklady:

Př.1

Př.2

Rozklady mnohočlenů

Rozkladem mnohočlenu rozumíme jeho zápis ve tvaru součinu několika mnohočlenů nižších stupňů.

Základní metody rozkladu:

1. Vytýkání společného jednočlenu před závorku

Tímto jednočlenem dělíme každý člen mnohočlenu.

2. Postupné vytýkání

Vhodně spojíme členy mnohočlenu do skupin a z těchto nově vzniklých mnohočlenů vytýkáme. Objevíme-li v nových mnohočlenech společné mnohočleny, postup zopakujeme.

3. Užití vztahů

4. Rozklad kvadratického trojčlenu

Některé kvadratické trojčleny lze rozkládat v oboru celých čísel Z.

Platí:

1)

ax2 + bx + c = a(x – x1)(x – x2), kde x1, x2 jsou kořeny rovnice ax2 + bx + c = 0, tedy

2)

ax2 + bx + c = a(x – x1)(x – x2), kde pro x1, x2 platí

(Vietovy vzorce)

Nejmenší společný násobek a největší společný dělitel dvou nebo několika mnohočlenů

Nejmenší společný násobek n dvou nebo více mnohočlenů získáme podobně jako u přirozených čísel, jestliže z rozkladů mnohočlenů vybereme mnohočleny, které se vyskytují alespoň v jednom rozkladu, a to s nejvyšší mocninou, ve které se mnohočleny rozkladech vyskytuje, a tyto mocniny mnohočlenů vynásobíme.

Největší společný dělitel D dvou nebo více mnohočlenů získáme opět jako u přirozených čísel, jestliže z rozkladů mnohočlenů vybereme mnohočleny, které se vyskytují v rozkladu každého mnohočlenu alespoň jednou, a to s nejnižší mocninou, v níž se mnohočlen v rozkladu vyskytuje, a tyto mocniny mnohočlenů vynásobíme.