Racionální čísla

D: Racionální čísla jsou všechna čísla, která lze zapsat ve tvaru zlomku 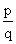, kde p je celé číslo a q je přirozené číslo. Množinu (obor) racionálních čísel označujeme Q.

Pro každá tři racionální čísla a, b, c platí:
Věty  o uzavřenosti	sčítání	Součet a + b je racionální číslo
	násobení	Součin a . b je racionální číslo
	odčítání	Rozdíl a – b je racionální číslo
	dělení	Podíl a : b, kde je racionální číslo
Věty  o komutativnosti	sčítání	a + b = b + a
	násobení	a.b = b.a
Věty o asociativnosti	sčítání	(a + b) + c = a + (b + c)
	násobení	(a.b).c = a.(b.c)
Věta  o neutrálnosti	čísla 1 vzhledem k násobení	a.1 = a
	čísla 0 vzhledem ke sčítání	a + 0 = a
Věta  o distributivnosti	násobení vzhledem ke sčítání	a.(b + c) = a.b + a.c

Číslo převrácené k číslu a, kde 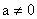, je číslo 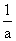. Odtud plyne, že převrácené číslo k číslu 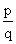 je čísl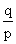o  pro .

Vyjádření racionálního čísla, ve kterém p a q jsou čísla nesoudělná (nemají společného dělitele) nazýváme vyjádření racionálního čísla v základním tvaru.

Porovnávání racionálních čísel a základní početní výkony se zlomky

(pro )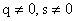

Zápis racionálního čísla

Desetinným číslem se rozumí racionální číslo, které lze zapsat tzv. desetinným zlomkem ve tvaru 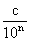, kde c je celé číslo a n přirozené číslo. Jde tedy o číslo s konečným desetinným rozvojem.

Racionální čísla můžeme zapisovat ve tvaru zlomku, desetinného čísla, nebo čísla s nekonečným periodickým desetinným rozvojem s vyznačenou periodou.