Výroková logika a teorie množin

Výrok: Každé sdělení, o kterém můžeme rozhodnout, zda je či není pravdivé. Je-li výrok pravdivý, přiřazujeme mu 1.
             Není-li pravdivý, přiřazujeme mu 0. Výroky se označují velkými písmeny A, B, C, …, Z.

Logické spojky

Pomocí logických spojek vytváříme z jednoduchých výroků výroky složené.

Konjunkce (): „a“, „i“, „a zároveň“ – je pravdivá, když jsou pravdivé oba výroky
Disjunkce (): „nebo“ – je pravdivá, je-li pravdivý alespoň 1 výrok
Implikace (): „jestliže …, pak“ – není pravdivá jen tehdy, vyplývá-li z pravdy nepravda
Ekvivalence (oboustranná implikace) ()„…právě tehdy, když …“ – je pravdivá, mají-li oba výroky stejnou 
                                                                                                                       pravdivostní hodnotu

A	B
1	1	1	1	1	1
1	0	0	1	0	0
0	1	0	1	1	0
0	0	0	0	1	1

Negace výroku A je výrok, který má opačnou pravdivostní hodnotu než výrok A.

A
1	0
0	1

Negování složených výroků:

Kvantifikované výroky

Kvantifikované výroky jsou takové výroky, které udávají počet.

Obecný kvantifikátor (): „V každém…“, „Pro každé…“ – např.

Vyjadřuje, že každý uvažovaný objekt má (nebo žádný nemá) vlastnost o niž jde.

Existenční kvantifikátor (): „Existuje…“ – např.

Vyjadřuje, že alespoň jeden objekt má vlastnost o kterou jde.

Jednoduchý kvantifikovaný výrok	Jeho negace
Každý . . . je . . . Všech n (každý z n) . . . je . . . (nN, n > 1)	Alespoň jeden . . . není . . . Alespoň jeden z n . . . není . . .
Alespoň jeden . . . je . . . Alespoň n . . . je . . . (nN, n > 1)	Žádný . . . není . . . Nejvýše n – 1 . . . je . . .
Nejvýše n . . . je . . . (nN, n >1)	Alespoň n + 1 . . . je . . .
Právě jeden . . . je . . . Právě n . . . je . . . (nN, n > 1)	Žádný . . . není . . . nebo alespoň dva . . . jsou . . . Nejvýše n – 1 . . . je . . . nebo alespoň n + 1 . . . je . . .

Množiny a operace s nimi

Množina: Soubor (souhrn) libovolných různých objektů, které mají vlastnost, podle níž můžeme rozhodnout, zda do množiny patří nebo nepatří. Pak tyto objekty nazýváme prvky množiny. K označení množin užíváme zpravidla velkých písmen abecedy (A, B, C, D, …..), prvky označujeme obvykle malými písmeny (a, b, c, d, …).

Určení množin:

- výčtem, tj. uvedením všech jejich prvků

- užitím charakteristické vlastnosti

Množiny znázorňujeme pomocí tzv. Vennových diagramů.

Prázdná množina je taková množina, která neobsahuje žádný prvek. Označuje se obvykle nebo .

Vztahy mezi množinami

Podmnožina (): „A je podmnožinou B“ – inkluze

Rovnost (A = B):

nebo-li

Operace s množinami

Vennovy diagramy:  U – základní (univerzální) množina

Sjednocení :

Průnik :

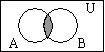
Rozdíl :

Doplněk množiny A v množině B :

Doplněk množiny A v základní množině U (A´):

de Morganova pravidla: