Mechanické kmitání

Kmitavý pohyb (mechanické kmitání) je takový pohyb, kdy se těleso nebo hmotný bod pohybuje po úsečce nebo kruhovém oblouku kolem rovnovážné polohy. Jestliže rovnovážnou polohou prochází v pravidelných časových intervalech, koná periodický kmitavý pohyb. Takový pohyb vykonává např. těleso zavěšené na pružině, písty v motoru apod.

Rovnovážná poloha je taková poloha, kde má těleso nejmenší potenciální energii. Po skončení pohybu těleso zůstává v rovnovážné poloze, dokud na něj nezačne působit vnější síla.

Mechanická soustava, která vykonává kmitavý pohyb se nazývá mechanický oscilátor. Mechanický oscilátor může být závaží zavěšené na pružině, kyvadlo apod.

Kyvadlo je těleso zavěšené nad těžištěm, které kmitá kolem své rovnovážné polohy po kruhovém oblouku, jehož středem je osa procházející závěsem.

Kinematika kmitavého pohybu

Základní veličina, která popisuje periodické pohyby je perioda T. Je to čas, po kterém se periodický pohyb opakuje. [T] = s

Počet opakování za jednotku času je frekvence (kmitočet) f. [f] = s^–1 = Hz (hertz)

Nejjednodušší kmitavý pohyb je harmonický pohyb. Je to takový pohyb, kdy je okamžitá výchylka z rovnovážné polohy závislá na funkci sinus,

popř. cosinus.

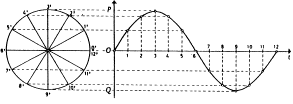Grafem výchylky harmonického pohybu v závislosti na čase je sinusoida.

Harmonický kmitavý pohyb je pravoúhlý průmět rovnoměrného pohybu po kružnici. Rovnovážná poloha je ve středu kružnice.

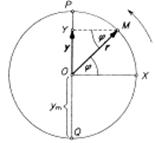
Při pohybu mechanického oscilátoru se okamžitá výchylka y periodicky mění a vzhledem k rovnovážné poloze nabývá kladných i záporných hodnot. V určitých časech dosahuje y největší kladné, popř. záporné hodnoty. Absolutní hodnota největší výchylky je amplituda výchylky y_m.

Když necháme obíhat hmotný bod po obvodu kružnice, jejíž střed umístíme do počátku soustavy souřadnic, jeho polohu popisuje vektor r, který má počáteční bod ve středu kružnice a koncový v hmotném bodě.

Okamžitá výchylka y je pak průmět vektoru r do osy y. Když hmotný bod urazí na kružnici úhel j od osy x, platí pro y:

Úhel j ([j] = rad) se nazývá fáze kmitavého pohybu a určuje v každém okamžiku jednoznačně okamžitou výchylku. Platí pro něj:

,

kde w je úhlová frekvence. Je to úhel, který hmotný bod urazí za jednotku času, [w] = rad × s^–1

Když vektor r leží v ose y, určuje největší výchylku hmotného bodu z rovnovážné polohy. Odpovídá tedy amplitudě výchylky:  r = y_m

Pro okamžitou výchylku platí vztah:

Popisuje okamžitou výchylku kmitavého pohybu tělesa, které se v počátečním okamžiku nachází v rovnovážné poloze.

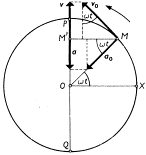Rychlost a zrychlení harmonického pohybu

Rychlost harmonického pohybu je změna výchylky za čas

Z uvedeného vztahu vyplývá, že rychlost je derivace okamžité výchylky podle času

Rychlost harmonického pohybu bude největší v rovnovážné poloze, v amplitudě výchylky bude nulová. Největší rychlost harmonického pohybu je amplituda rychlostí v_m

v_m = w × y_m

Podobně zrychlení harmonického pohybuj je změna rychlosti za čas

Zrychlení je derivace rychlosti podle času

Zrychlení harmonického pohybu směřuje proti výchylce, největší je v amplitudě, nulové v rovnovážné poloze. Zrychlení harmonického pohybu je přímo úměrné okamžité výchylce a v každém okamžiku má opačný směr. Největší zrychlení harmonického pohybu je amplituda zrychlení a_m

a_m = w² × y_m

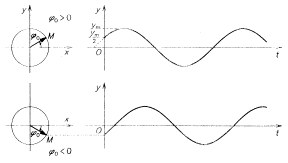Když harmonický pohyb nezačíná v rovnovážné poloze, musíme uvažovat, že v čase t = 0 už hmotný bod urazil úhel j₀. j₀ je počáteční fáze kmitavého pohybu. Pro okamžitou výchylku kmitavého pohybu s počáteční fází bude platit

Pro znázornění počáteční fáze se používá fázorový diagram, kde se využívá souvislosti mezi rovnoměrným pohybem po kružnici a harmonickým pohybem. Fázorový diagram má význam hlavně pro skládání kmitů. Základní vlastnosti 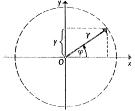harmonického pohybu – amplitudu výchylky a počáteční fázi – zobrazí fázor – vektor s počátkem ve středu diagramu, jeho délka odpovídá amplitudě, úhel mezi ním a osou x počáteční fázi.

Při srovnávání dvou harmonických pohybů je důležitý jejich fázový rozdíl Dj. Je to posun, který je mezi dvěma harmonickými pohyby.

Dj = j₀₂ – j₀₁

j₀₁ a j₀₂ jsou počáteční fáze obou pohybů.

Fázový rozdíl výchylky a rychlosti je p/2 rad a výchylky a zrychlení p rad.

Je-li fázový rozdíl dvou harmonických pohybů 2×k×p rad, mají pohyby stejnou fázi a pro (2×k+1)×p rad opačnou fázi.

Složené kmitání

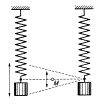Když spojíme dva oscilátory vláknem, jehož střed zvýrazníme, a rozkmitáme oscilátory, uvidíme, že i střed vlákna kmitá. Jeho kmity odpovídají pohybu vzniklému složením kmitů obou oscilátorů. Vzniká složené kmitání. Stejně jako pro ostatní pohyby i pro kmitání platí princip superpozice:

Jestliže hmotný bod koná současně několik harmonických kmitavých pohybů, téhož směru s okamžitými výchylkami y₁, y₂, …, y_k, je okamžitá výchylka y výsledného kmitání

y = y₁ + y₂ + … + y_k

Okamžité výchylky mohou mít kladnou i zápornou hodnotu.

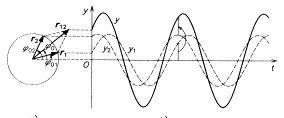Skládají-li se harmonické pohyby se stejnou frekvencí, vznikne harmonický pohyb se stejnou frekvencí. U takového skládání se musí uvažovat jen s amplitudou a počáteční fází. Tyto veličiny se zobrazují fázory, proto je výhodné pro skládání kmitů používat fázorový diagram, kde jednotlivým harmonickým pohybům přísluší fázory. Výsledný pohyb, jeho amplituda a počáteční fáze se určí vektorovým součtem.

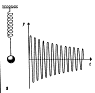
Pokud mají jednotlivé kmity různou frekvenci, vzniknou poměrně složité kmity s neharmonickým průběhem.

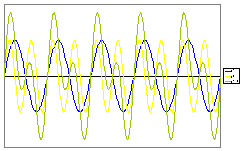
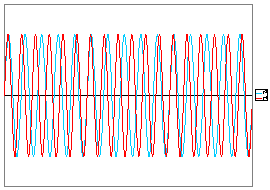
Zvláštní případ nastane, když obě frekvence jsou přibližně stejně velké (w₁ → w₂). Amplituda výchylky výsledného pohybu se periodicky zvětšuje a zmenšuje. Vzniká složené kmitání, které nazýváme rázy. Amplituda rázů se mění s frekvencí f = f₂ – f₁. Na obrázku jsou rázy vzniklé složením kmitů o poměru frekvencí 1,2 : 1. Rázů se využívá pro ladění.

       

 

Dynamika kmitavého pohybu

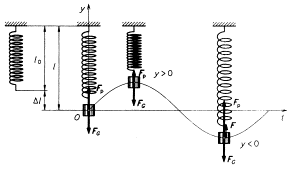Podle druhého Newtonova zákona je celková síla, která způsobuje harmonické kmitání

Tato rovnice se také nazývá pohybová rovnice harmonického pohybu. Úhlová frekvence oscilátoru však závisí na jeho vlastnostech, které určují parametry oscilátoru. Je-li oscilátor závaží zavěšené na pružině, pak jeho parametry jsou hmotnost tělesa m a tuhost pružiny k.

K tomu, aby se pružina z původní délky l₀ prodloužila na délku l = l₀ + Dl, ji musíme deformovat silou F = k × Dl. Tuhost pružiny je definována vztahem

Tuhost pružiny je tím větší, čím větší sílu potřebujeme k jejímu prodloužení o stejnou délku. [k] = N × m^–1

Když na pružinu o tuhosti k zavěsíme těleso o hmotnosti m, pak se pružina prodlouží o Dl. Těleso se ustálí v rovnovážné poloze, takže výslednice sil na něj působících je nulová. Působí jen síla pružnosti F_p = k × Dl a tíhová síla tělesa F_G = m × g . Bude proto platit

k × Dl = m × g

Uvedeme-li oscilátor do kmitavého pohybu, bude velikost výsledné síly na těleso působící

Na těleso mechanického oscilátoru působí proměnlivá síla o velikosti

F = – k × y,

která stále směřuje do rovnovážné polohy a je příčinou kmitavého pohybu oscilátoru.

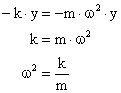
Úhlová frekvence volně kmitajícího mechanického oscilátoru závisí jen na jeho parametrech, tj. na hmotnosti m tělesa a tuhosti pružiny k. Takové kmitání nazýváme vlastní kmitání oscilátoru a jeho úhlovou frekvenci označíme w₀:

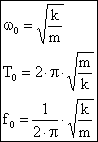
Pomocí uvedených vztahů lze určit setrvačnou hmotnost tělesa, tzn. určit hmotnost tělesa v pohybu {laboratorní práce}.

Kyvadlo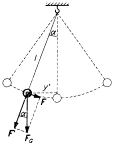

Fyzické kyvadlo je jakékoli těleso zavěšené nad těžištěm, které se může otáčet kolem vodorovné osy nad těžištěm. Matematické kyvadlo je myšlenkový model. Je to hmotný bod zavěšený na tenkém vlákně se zanedbatelnou hmotností a zanedbává se i odpor prostředí a deformace vlákna. Ve skutečnosti se matematickému kyvadlu blíží závaží zavěšené na tenkém provázku.

Když kyvadlo necháme kmitat tak, aby výchylka nepřekročila 5°, můžeme pohyb hmotného bodu považovat se pohyb přímočarý. Na hmotný bod působí tíhová síla F_G, která se při vychýlení z rovnovážné polohy rozkládá na sílu F´, která napíná lanko a na sílu F, která způsobuje, že se hmotný bod snaží vrátit do rovnovážné polohy.

Platí:

y´ je vzdálenost hmotného bodu od svislé roviny, v níž se nachází rovnovážná poloha. y je velikost výchylky hmotného bodu tzn. velikost oblouku kružnice, o který se hmotný bod vychýlí z rovnovážné polohy.

Kyvadlo má vlastnosti mechanického oscilátoru, pro který platí

Při prvním pohledu na obě poslední rovnice je patrná obdoba:

Po dosazení do vztahu pro periodu mech. oscilátoru:

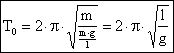
Perioda matematického kyvadla závisí jen na délce závěsu a na tíhovém zrychlení. Tak lze periodu pohybu kyvadla určit délkou závěsu nebo pomocí kyvadla určit tíhové zrychlení v daném místě {laboratorní cvičení}.

Důležitý pojem v souvislosti s měřením času je i kyv t, který je roven polovině periody t = T/2. Kyv je doba za kterou kyvadlo projde z jednoho maxima do druhého. Sekundové kyvadlo má kyv 1 sekundu.

Přeměny energie v mech. oscilátoru

Celková energie mechanického oscilátoru se skládá z kinetické energie E_k, z tíhové potenciální energie E_pt a potenciální energie pružnosti E_pr.

Kinetická energie je

Tíhová potenciální energie je

E_pt = m × g × h

Potenciální energie pružnosti je

Klidová energie oscilátoru je

Když mech. oscilátor uvedeme do kmitavého pohybu, zvětší se jeho celková energie E_celk o energii kmitání. Při okamžité výchylce y má oscilátor okamžitou rychlost v a platí:

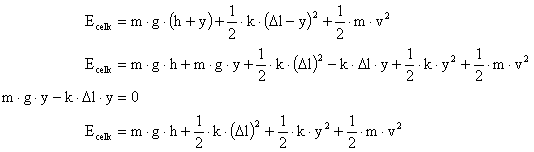
Když celkovou energii rozdělíme na klidovou energii a energii kmitání, bude energie kmitání:

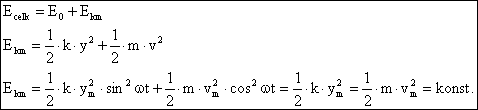
Při harmonickém pohybu se periodicky mění potenciální energie kmitání v energii kinetickou a naopak. Celková energie oscilátoru je konstantní a je rovna součtu klidové energie oscilátoru energie kmitání dodané oscilátoru při uvedení do kmitavého pohybu. Energie kmitání je přímo úměrná druhé mocnině amplitudy výchylky a druhé mocnině úhlové frekvence vlastního kmitání.

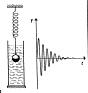
Až doposud jsme uvažovali, že na mech. oscilátor nepůsobí žádné vnější síly. Ve skutečnosti však působí odpor prostředí, proto se amplituda postupně zmenšuje, až je nakonec nulová. Energie se mění na jiné formy než mechanickou – většinou na vnitřní energii → ohřeje oscilátor a prostředí). Kmitání, u kterého se zmenšuje amplituda, se nazývá tlumené kmitání. Na míru tlumení má vliv prostředí. Při kmitání ve vzduchu se amplituda výchylky zmenšuje velmi pomalu, ve vodě rychleji. Kdyby oscilátor kmital v medu, neudělal by ani jednu periodu.

Vlastní kmitání oscilátoru je vždy tlumené. Abychom získali netlumené kmity, musíme na oscilátor působit silou, aby se kmity netlumily. Takové kmity se nazývají nucené kmitání mech. oscilátoru. Při nuceném kmitání oscilátor kmitá vždy s frekvencí vnějšího působení. Nucené kmitání vzniká působením periodické síly na oscilátory i na objekty, které vlastnosti oscilátoru nemají. Frekvence nuceného kmitání závisí na frekvenci působící síly a nezávisí na vlastnostech kmitajícího objektu. Nucené kmitání je netlumené.

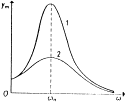Když se frekvence nutící síly přiblíží vlastní frekvenci oscilátoru, velmi se zvětší amplituda kmitů. Dojde k rezonanci. Měníme-li frekvenci nutící síly, pak v hodnotě frekvence vlastních kmitů je amplituda největší – vznikne maximum. Maximum je tím ostřejší, čím méně se tlumí vlastní kmity. Graf závislosti amplitudy nucených kmitů na frekvenci nutících kmitů je rezonanční křivka. Rezonanční frekvence se poněkud zmenšuje s rostoucím tlumením.

Význam rezonance spočívá v tom, že umožňuje rezonanční zesílení kmitů. Malou, periodicky působící sílou lze v oscilátoru vzbudit kmitání o značné amplitudě výchylky, pokud je perioda vnějšího působení shodná s periodou vlastního kmitání oscilátoru.

Rezonance je využita např. u hudebních nástrojů.