Studuje zákonitosti pohybu kapalin. Její obdobou pro plyny je aerodynamika.
Vlastnosti kapalin a plynů
Společná základní vlastnost je tekutost (→ kapaliny a plyny – tekutiny). Její příčinou je snadná vzájemná pohyblivost částic, z nichž se kapaliny skládají. Kapalná a plynná tělesa nemají stálý tvar, přizpůsobují se tvaru okolních pevných těles – tvaru nádoby, rozlévají se po stole, přehrazené řeky vyplňují údolí. Plyny vyplňují nádoby, v nichž jsou umístěny.
Kapaliny zachovávají stálý objem a jsou velmi málo stlačitelné. Jsou-li kapaliny v klidu, pak v tíhové m poli Země vytvářejí vodorovný povrch – volnou hladinu.
Plyny nemají stálý tvar ani stálý objem, jsou velmi snadno stlačitelné. Vzdálenosti mezi molekulami plynu jsou mnohem větší než u kapalin, což umožňuje jejich stlačení. Tvar a objem jsou dány tvarem a objemem nádoby, v nichž je plyn umístěn. Zvětšíme-li objem tělesa, plyn vyplní opět celý objem nádoby.
Různé kapaliny a plyny se liší svou tekutostí. Z kapalin je značný rozdíl mezi vodou a medem (med stéká ze lžičky velmi pomalu). Tekutější kapaliny mají menší vnitřní tření – viskozitu (tření vznikající smýkáním molekul po jiných molekulách). Viskozita plynů je mnohem menší než viskozita kapalin.
Pro zjednodušení se zavedly:
Ideální kapalina – dokonale tekutá, bez vnitřního tření, zcela nestlačitelná
Ideální plyn – dokonale tekutý, bez vnitřního tření, dokonale stlačitelný
Proudění je takový pohyb tekutin, kdy u částic převažuje pohyb v jednom směru. Proudí např. voda v řekách a potocích, voda a plyn potrubím.
Pohyb tekutin je složitější než pohyb pevných látek, protože jednotlivé částice mohou měnit vzájemnou polohu. Každá částice v proudící tekutině má určitou rychlost v, jejíž velikost a směr se může v závislosti na místě a čase měnit. Pokud je rychlost v částic stálá, jde o ustálené, neboli stacionární proudění.
Trajektorie jednotlivých částic proudící tekutiny znázorňujeme proudnicemi. Proudnice je myšlená čára, jejíž tečna v libovolném bodě má směr rychlosti v pohybující se částice. Každým bodem proudící tekutiny prochází při ustáleném proudění jen jedna proudnice Þ proudnice se nemohou navzájem protínat.
Proudové vlákno je průřez trubice, kterou proudí kapalina; plocha, kterou proudí kapalina.
Ustálené proudění ideální kapaliny je nejjednodušším případem proudění kapalin. Při něm protéká každým průřezem trubice stejný objem kapaliny.
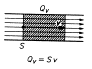Objem kapaliny, který proteče daným průřezem trubice za jednotku času se nazývá objemový průtok QV. Protéká-li průřezem o plošném obsahu S kapalina rychlostí v, je objemový průtok
QV = S × v
[QV] = m3 × s–1
Objem vody, který potrubím proteče za libovolnou dobu měříme vodoměrem, objem plynu plynoměrem.
Ideální kapalina je nestlačitelná, proto se na žádném místě nemůže hromadit, proto je objemový průtok v každém průřezu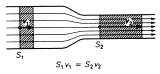 
stejný. Platí QV = konst., což je rovnice spojitosti toku neboli rovnice kontinuity:
S1×v1 = S2 ×v2 = S × v = konst.
Při ustáleném proudění ideální kapaliny je součin obsahu průřezu S a rychlosti proudu v v každém místě trubice stejný.
V místě, kde se zúží průřez trubice, se zvětší rychlost proudění. Toho lze využít na zahradě, když chceme dostříknout dál – stačí hadici zčásti ucpat.
Plyny však jsou stlačitelné, a proto má pro ně větší význam veličina hmotnostní průtok Qm. Hmotnostní průtok vyjadřuje hmotnost látky, která projde průřezem trubice za jednotku času. [Qm] = kg × s–1 Mezi hmotnostním a objemovým průtokem je vztah:
Qm = r × QV
Ideální kapalina má konstantní hustotu, proto v rovnici spojitosti stačí uvažovat s objemem, ale u plynů jejich hustota závisí na míře stlačení. Hmotnostní průtok se nemění ani u plynů (vychází to ze zákona zachování hmotnosti). Rovnice kontinuity kapalin i plynů:
Qm = konst.; r1 × S1 × v1 = r2 × S2 × v2 = r × S × v = konst.
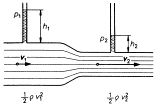
Bernoulliho rovnice vyjadřuje zákon zachování energie pro proudění ideální kapaliny ve vodorovném potrubí.
Když se ve zúženém místě zvětší rychlost kapaliny, získá větší kinetickou energii. Podle zákona zachování energie tato kinetická energie DEk vzniknout přeměnou z potenciální energie, která se kvůli tomu zmenší o DEp, o níž platí, že DEk = DEp .
Uvažujeme-li, že trubice je vodorovná, nemůže jít o potenciální energii tíhovou. Ideální kapalina je nestlačitelná, proto nelze uvažovat ani potenciální energii pružnosti. U proudící kapaliny se jedná o změnu, která souvisí s tlakem proudící kapaliny ® tlaková potenciální energie.
Velikost tlakové potenciální síly zjistíme-li necháme-li tlakovou sílu F působit na píst. Pokud se velikost F nemění, pak když posune píst o obsahu S vodorovným potrubím o délku l, vykoná práci
W = F × l .
Síla je vyvolaná tlakem, proto platí
F = p × S .
Když dosadíme do vzorce,
W = p × S × l,
objem trubice, o který se píst posunul, je
V = S × l,
proto
W = p × V
Tlaková potenciální energie kapaliny:
Ep = p × V
Kinetická energie:
Podle zákona zachování energie platí:
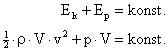
Po vydělení rovnice objemem V:
První člen rovnice je kinetická energie proudící kapaliny o jednotkovém objemu, druhý člen je tlaková potenciální energie proudící kapaliny o jednotkovém objemu (rovná se tlaku kapaliny).
Součet kinetické a tlakové potenciální energie kapaliny o jednotkovém objemu je ve všech částech vodorovné trubice stejný.
Chceme-li zobecnit Bernoulliho rovnici i pro nevodorovnou trubici, musíme uvažovat i s tíhovou potenciální energií kapaliny
E = m × g × h = r × V × g × h ;
převedeno na jednotkový objem získáme člen r × g × h
Důsledků Bernoulliho rovnice se využívá v Pitotově trubici:
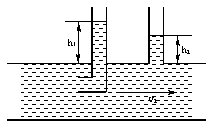
Pomocí Pitotovy trubice se určuje rychlost proudící kapaliny pomocí rozdílu tlaků. Kapalina v ohnutém vývodu ztratí veškerou svou rychlost, zatímco u rovného vývodu má kapalina stále svou rychlost. Svou energii si uchová, proto bude platit:
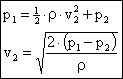
Rozdíl tlaků se určí z rozdílu hladin v obou vývodech →
Způsob měření rychlosti tímto způsobem se používá u letadel.
Když velmi zúžíme průřez trubice, podle rovnice spojitosti začne rychlost proudící kapaliny nabývat velkých hodnot, takže hodnota absolutního tlaku kapaliny (tento tlak se skládá z tlaku způsobeného vnější silou, z hydrostatického tlaku a v atmosféře Země navíc z atmosférického tlaku) může klesnout až pod hodnotu atmosférického tlaku a vznikne tak podtlak.
Na principu podtlaku procuje rozprašovač (v karburátoru) nebo vývěva.
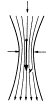Snížení tlaku v zúžené trubici (důsledek rovnice spojitosti – v menším průřezu se rychlost proudění zrychlí –, a Bernoulliho rovnice – zvýšení rychlosti proudící kapaliny vede ke zmenšení tlaku) bylo nazváno hydrodynamické paradoxon.
Když foukne mezi dva listy papíru, proudící vzduch vyvolá podtlak a listy se přitahují → aerodynamické paradoxon.
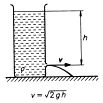Ze zákona zachování hmotnosti lze určit také rychlost kapaliny, která vytéká otvorem v nádobě v hloubce h pod hladinou kapaliny. Platí zde zákon zachování energie, mění se tíhová potenciální na kinematickou – u kapaliny energie na jednotkový objem.
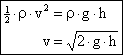
Výše uvedené zákonitosti proudění tekutin platí pro ideální tekutiny, ale ve skutečnosti neplatí úplně přesně. Zvláště v reálné kapalině působí vždy proti pohybu částic odporové síly způsobené vnitřním třením (viskozitou) kapaliny u plynů se neprojevují tak znatelně kvůli nízké viskozitě.
Ideální kapalina měla v každém bodě průřezu stejnou rychlost. Ale u reálné kapaliny se částice, které se pohybují středem trubice, pohybují rychleji než ty, které se pohybují blíže ke stěně trubice a nejpomalejší jsou ty, které se jí přímo dotýkají - částice na tzv. mezní vrstvě kapaliny. Rozdílné rychlosti způsobuje rozdílné tření.
Při malých rychlostech proudění jsou proudnice stále ještě rovnoběžné → laminární proudění.
Ale při vyšších rychlostech se kvůli rozdílům v rychlosti pohybu částic tvoří víry → turbulentní proudění. Pro překonání odporu kapaliny se žene potrubím pomocí čerpadel → zvýšení tlaku.
Obtékání těles reálnou tekutinou
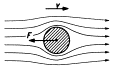Když se těleso pohybuje vzhledem k tekutině, v níž je, dojde k obtékání. Při obtékání působí tření mezi tělesem a tekutinou Þ hydrodynamická (u kapalin) a aerodynamická (u plynů) odporová síla ® odpor prostředí.
Při malých rychlostech je proudění kolem těles laminární a odporová síla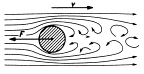 
F je poměrně malá a roste přímo úměrně relativní rychlosti v (tělesa vzhledem k prostředí). Při větších rychlostech vzniká proudění turbulentní, velikost odporové síly F se zvětšuje už s druhou mocninou rychlosti v. Pro velikost aerodynamické odporové síly odvodil Newton vztah
,
kde C je součinitel odporu pro daný tvar tělesa, r hustota plynu, S obsah průřezu tělesa kolmého ke směru pohybu a v relativní rychlost.
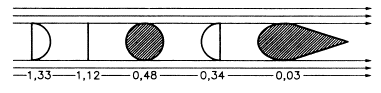
Největší odpor má dutá polokoule (padáky), nejmenší těleso proudnicového neboli aerodynamického tvaru (ptáci, letadla, ve největší možné auta, ale zde značné rozdíly – kamion × formule 1 – kamion má do aerodynamického tvaru daleko).
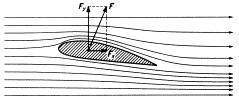
Křídla malých letadel jsou také aerodynamického tvaru, ale nejsou souměrná. Horní plocha je větší než spodní, proto ji vzduch obtéká rychleji. Podle Bernoulliho rovnice je větší tlak na spodní plochu křídla a na celou nosnou plochu křídla pak působí vztlaková aerodynamická síla Fy. Dále na křídlo působí ještě odporová síla Fx, kterou překonává tah motorů. Jejich výslednicí je výsledná aerodynamická síla F.
Newtonův vztah pro odporovou sílu platí je pro středně velké rychlosti. Pro větší, než je rychlost šíření zvuku, je rychlost odporové síly úměrná třetí mocnině rychlosti v. Těleso vytváří rázovou vlnu – rány při přeletu nadzvukových letadel.