Dynamika hmotného bodu

Dynamika je obor mechaniky, který se zabývá příčinami změn pohybového stavu těles.

Hmotný bod – je myšlený bodový objekt, který má hmotnost, ale nemá rozměry

– nahrazujeme jím těleso, pokud jeho rozměry jsou zanedbatelné vzhledem k uvažovaným vzdálenostem pohybu, hmotný bod se umísťuje do těžiště tělesa, má jeho hmotnost

– používáme ho pro zjednodušení.

Vztažná soustava –umístění HB v prostoru a čase, zavedené čtyři souřadnice: x, y, z, čas t.

Inerciální vztažnou soustavu používáme pro pohyby, probíhající na povrchu Země nebo v její blízkosti, vztažná soustava je spojena s povrchem Země. Platí zde mechanický princip relativity – Galileiho princip relativity a Newtonovy zákony.

Zákony mechaniky jsou stejné ve všech inerciálních vztažných soustavách. Rovnice, které je vyjadřují, mají stejný tvar.

Pokud jedeme vlakem, který se pohybuje rovnoměrným přímočarým pohybem a nemáme možnost vidět ven, nepoznáme, zda je daná soustava vzhledem k povrchu země v klidu nebo v pohybu.

Všechny inerciální vztažné soustavy jsou pro popis mechanických dějů rovnocenné.

Neinerciální vztažná soustava je taková soustava, která se vzhledem k inerciální vztažné soustavě pohybuje jinak než rovnoměrně přímočaře. Nejjednodušší je ta, která se vzhledem k inerciální vztažné soustavě pohybuje rovnoměrně zrychleným přímočarým pohybem a má konstantní zrychlení.

Neplatí zde Newtonovy pohybové zákony. Pokud jedeme vlakem, který se pohybuje rovnoměrným zrychleným pohybem, poznáme to mechanickým pokusem (kulička na podlaze vagónu). Na kuličku působí síla :

F_s = – m × a

Tato síla se nazývá setrvačná síla.

V neinerciálních vztažných soustavách nezůstává izolované těleso v klidu nebo v rovnoměrně přímočarém pohybu. Na těleso v neinerciální vztažné soustavě působí setrvačná síla

F_s = – m× a ,

vznikající jako důsledek zrychleného pohybu soustavy,

Setrvačné síly existují jen v neinerciálních vztažných soustavách.

Setrvačná síla se projevuje v rozjíždějícím se nebo zastavujícím vlaku. Ten má vůči zemi zrychlení a. Položíme-li na podlahu vlaku kuličku, bude vůči zemi dál v klidu. Ale vlak se pohybuje se zrychlením, proto se kulička vzhledem k vlaku bude pohybovat se zrychlením – a. Při rozjíždění vlaku pojede dozadu, při zastavování vpřed – stejně to cítí i cestující.

Soustava se může vzhledem k zemi pohybovat i rovnoměrně zrychleně ve svislém směru, např. kabina výtahu. I zde se projevuje působení setrvačné síly. Zrychlení ve směru vzhůru (rozjezd nahoru a brzdění dolů) se projevuje přetížením a ve směru dolů (brzdění při jízdě nahoru a rozjezd při jízdě dolů) se projevuje úbytkem tíže. Při volném pádu se tělesa ve výtahu ocitají ve stavu beztíže (na tělesa působí tíha a setrvačná síla, které se vzájemně zruší).

Vzájemné působení těles

Tělesa na sebe vzájemně působí silami. K působení dojde buď přímým stykem nebo prostřednictvím silových polí. Přímým stykem působí síly nárazem nebo tlakem, při působení polí je působení gravitace, elektrického pole či magnetického pole. Gravitace se projevuje při pádu těles – tělesa se Země ani ničeho jiného nedotýkají, přesto jsou přitahovány. Působení síly může mít za následek deformaci tělesa (deformační účinek síly) nebo změnu pohybového stavu tělesa (pohybový účinek síly).

Síla F je vektorová fyzikální veličina. Účinek síly závisí na její velikosti, směru a poloze působiště.

[F] = N (newton) = m × kg × s^–2 Vektor síly má stejný směr jako okamžité zrychlení.

Newtonovy pohybové zákony

Izolované těleso (HB) je takové těleso (HB), na které nepůsobí žádné síly. Izolované těleso, které je v dané vztažné soustavě v klidu, setrvává v klidu.

Izolované těleso, které je v pohybu, má stále stejnou rychlost, pohybuje se rovnoměrným přímočarým pohybem. Izolované těleso, které je v klidu, zůstává v klidu

Izolovaná soustava je taková soustava, kde mezi silami těles nepůsobí síly ze vnějšku.

1. Zákon setrvačnosti

Každé těleso setrvává v klidu nebo v rovnoměrně přímočarém pohybu, pokud není nuceno vnějšími silami tento stav změnit.

Tento zákon je základním předpokladem pro potvrzení, že daná soustava je inerciální. Důsledkem tohoto zákona je rovnoměrný přímočarý pohyb, který charakterizuje nulové zrychlení. V praxi se rovnoměrně přímočaře pohybují sondy v meziplanetárním prostoru, protože na ně nepůsobí síly dost velké na to, aby je znatelně zpomalily. Na Zemi se pohybu rovnoměrného přímočarého dosahuje tak, že výslednice všech sil působících na těleso je rovna nule. Výslednice sil je taková síla, která má na HB stejný účinek jako všechny síly na něj působící.

2. Zákon síly

Velikost zrychlení hmotného bodu je přímo úměrná velikosti výslednice sil působících na hmotný bod, a nepřímo úměrná hmotnosti hmotného bodu,

.

Směr zrychlení je shodný se směrem výslednice sil, vektorově je tedy

.

Začnou – li na těleso působit jiná tělesa silami, změní se pohybový stav tělesa. Těleso se začne pohybovat se zrychlením.

Důsledkem tohoto zákona je, že na všechna tělesa na Zemi působí tíhová síla

F_G = m × g.

Tato síla působí stejně jako tíhové zrychlení svisle dolů.

3. Zákon akce a reakce

Dvě tělesa na sebe navzájem působí stejně velkými silami opačného směru. Tyto síly vznikají a zanikají současně.

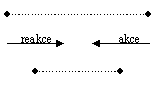Jednu z těchto sil nazýváme akce a druhou reakce. Akce a reakce působí každá na jiné těleso, proto se navzájem nezruší.

Dvě dívky jsou na kolečkových bruslích a drží opačné konce provazu. Jedna z nich zatáhne za provaz. Pohybovat se však nezačne jen druhá dívka, ale i ta, která za provaz zatáhla. Táhnoucí dívka vyvolala působením síly – akce, to že druhá síla – reakce bude působit na ni samotnou.

Hybnost hmotného bodu je vektorová fyzikální veličina, definovaná jako součin hmotnosti a okamžité rychlosti hmotného bodu.

p = m × v

[p] = kg × m × s^–1 (kilogram metr za sekundu)

Vektor hybnosti má stejný směr jako vektor okamžité rychlosti. Hybnost charakterizuje pohybový stav tělesa nebo HB v dané vztažné soustavě.

Změna hybnosti a impuls síly

Působí-li na těleso síla, pak podle zákona síly platí

F = m × a.

Podle definice zrychlení platí

.

Po dosazení

.

Změní-li se rychlost tělesa při konstantní hmotnosti, pak je změna hybnosti

.

Druhý pohybový zákon lze vyjádřit

.

Z tohoto vztahu lze vyjádřit

Dp = F × Dt.

Součin F × Dt síly a doby, kterou na těleso působila, je impuls síly. Její jednotkou je N × s (newton sekunda) a je to stejná jednotka jako jednotka hybnosti kilogram metr za sekundu.

Zákon zachování hybnosti: Celková hybnost izolované soustavy těles se vzájemným silovým působením těles nemění.

Celková hybnost soustavy je dána vektorovým součtem hybností obou těles :

p = p₁ + p₂

Tělesa na sebe působí akcí a reakcí. F₁ = –F₂. Podle druhého pohybového zákona platí:

p₁ – p₀₁ = – (p₂ – p₀₂)

p₀₁ + p₀₂ = p₁ + p₂

V izolované soustavě platí vedle zákona zachování hybnosti ještě zákon zachování hmotnosti:

Celková hmotnost izolované soustav těles je konstantní.

Celkovou hmotností soustavy rozumíme součet hmotností všech těles, z nichž se soustava skládá.

Po srážce dvou pohybujících se těles se obě tělesa budou pohybovat rychlostí v, kterou určíme vztahy:

p = (m₁ + m₂) × v = p₁ + p₂ = m₁ × v₁ + m₂ × v₂

Využití zákona zachování hybnosti

V moderním letectví a v kosmonautice se uplatňují reaktivní motory. Tryskami motoru unikají velkou rychlostí plyny vznikající při spalování pohonných látek. Podle zákona zachování hybnosti je raketa uvedena do pohybu opačným směrem. V elektrárnách se používají reaktivní turbíny. Zákon zachování hybnosti se také projevuje zpětným nárazem při střelbě ze střelných zbraní.

Smykové tření a valivý odpor

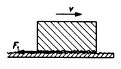Při posouvání neboli smýkání tělesa po povrchu jiného tělesa vzniká na styčné ploše obou těles třecí síla F_t, která směřuje vždy proti směru pohybu tělesa. Existence této síly znemožňuje experimentální potvrzení zákona setrvačnosti. Její velikost nezávisí na obsahu styčných ploch a při malých rychlostech na rychlosti tělesa, je přímo úměrná velikosti kolmé tlakové síly F_n a závisí na jakosti styčných ploch.

F_t = f × F_n

f je součinitel smykového tření, jehož velikost je různá pro různé dvojice materiálů (tabulky str. 161). [f] = 1 Je-li těleso na podložce v klidu, pak na ně působí klidové tření. Součinitel klidového tření f₀ je větší než součinitel smykového tření. (i jeho velikosti jsou v tabulkách str. 161). Velikost síly při klidovém tření: F_t = f₀ × F_n. Tření využíváme každodenně například při chůzi. Jaké to může být, když je tření mnohem menší lze snadno zjistit, stačí k tomu náledí. Přílišné tření je ale na škodu, proto se ložiska a další součástky, které jsou v častém kontaktu a pohybu s jinými, mažou olejem.

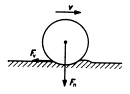Valivý odpor vzniká vždy, když se po podložce valí těleso kruhového průřezu. Působením kolmé tlakové síly F_n se poněkud deformuje těleso i podložka. Deformace vyvolává odporovou sílu F_v, která působí na těleso a směřuje proti směru pohybu. Velikost odporové síly je přímo úměrná velikosti kolmé tlakové síly F_n, nepřímo úměrná poloměru R valícího se tělesa a závisí také na jakosti povrchu.

x (ksí) je rameno valivého odporu. (tabulky str. 161) [x] = m

Valivý odpor je mnohem menší než smykové tření, čehož se využívá v praxi – snažíme se maximálně využít kol pro pohyb nákladu i nás samotných.

Dostředivá síla

Při rovnoměrném pohybu HB po kružnici má rychlost HB stálou velikost, ale mění se její směr. HB má dostředivé zrychlení a_d. Podle zákona síly je příčinou zrychlení HB vždy síla, která má stejný směr jako zrychlení. Rovnoměrný pohyb po kružnici způsobuje dostředivá síla F_d.

Po ukončení působení dostředivé síly se HB pohybuje ve směru okamžité rychlosti, která se už nemění. Směr pohybu tedy je po tečně ke kružnici v bodě ukončení působení dostředivé síly. K tomu dojde například když máme na provázku nějaký předmět a točíme a když se přetrhne provázek.

Pohybuje-li se soustava vzhledem k jiné po kružnici (např. auto v zatáčce vzhledem k zemi) pak tato soustava vzhledem k té druhé neinerciální – zemi považujme za soustavu v klidu a auto za neinerciální soustavu. Auto se pohybuje s dostředivým zrychlením a_d vzhledem k zemi. Jako v každé neinerciální soustavě i zde působí setrvačná síla F_s. Působí opět proti zrychlení, které charakterizuje pohyb soustavy. Zde charakterizuje pohyb dostředivé zrychlení, proto setrvačná síla směřuje od středu – odstředivá síla. Tato síla nás vytláčí ven ze zatáčky, když jí projíždíme.